数学コース
研究の紹介
|
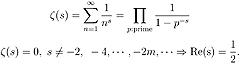 リーマン予想 |
|
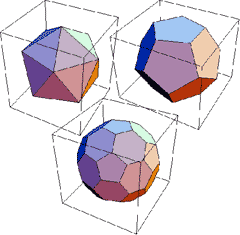 正多面体と準正多面体 |
|
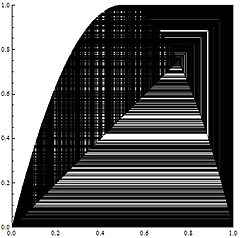 図1
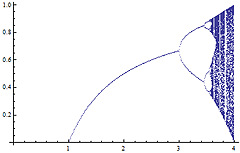 図2
|
|
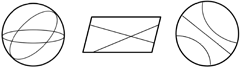 球面、平面および双曲平面(円板モデル)における直線(測地線) |
|
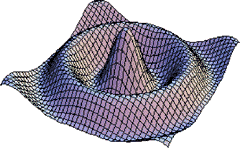 太鼓の音をベッセル関数で聞く |
|
 2次双曲面の変形 |
|
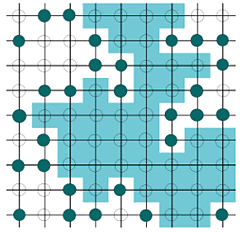 格子上の電子の配置(+スピンの連結成分) パーコレーションモデル |
|
|||||